Si tenemos en cuenta que los sentidos son los canales por los cuales accedemos a la información, surge casi inevitablemente la importancia de la “visualización” de los conceptos que aclara y facilita la comprensión y que además está estrechamente vinculada con modelos mentales intuitivos, simbolización y modelización, y es de gran utilidad para unir la intuición y el rigor requerido para el pensamiento matemático.
Las transformaciones lineales, se presentan muchas veces como conceptos abstractos, sin embargo muchas de ellas están presentes en la vida diaria como cuando “nos miramos al espejo”.
 Muchas de las transformaciones lineales que hemos estudiado, conservan la forma y las medidas de las figuras u objetos, como por ejemplo las simetrías y las rotaciones
Muchas de las transformaciones lineales que hemos estudiado, conservan la forma y las medidas de las figuras u objetos, como por ejemplo las simetrías y las rotaciones
otras sin embargo pueden modificar sus dimensiones como las homotecias y en algunos casos también sus formas como las proyecciones.
Con el software Matlab es posible visualizar los efectos que produce una transformación lineal sobre una figura. Los siguientes son ejemplos de archivos .m de comandos y de función que muestran algunos de estos efectos (en la cartilla tienen otros).
Pueden copiar el código y pegar en el editor de Matlab, luego lo guardan y desde la ventana de comandos lo ejecutan.
Ejemplo 1: Proyección de un triángulo sobre el plano XY
% PROYECCION DE UN TRIANGULO SOBRE EL PLANO XY
% Se ingresa en una matriz las componentes de los vertices de un triangulo en cada
% columna,repitiendo al final el primer vertice de manera que se cierre el triangulo
p=[3 0 2 3;1 -2 1 1;0 1 3 0];
% La primera fila de p corresponde a las componentes de los vertices en el eje X
% La segunda fila de p corresponde a las componentes de los vertices en el eje Y
% La tercera fila de p corresponde a las componentes de los vertices en el eje Z
% Se guardan estas filas en las variables x, y, z para poder realizar la grafica del triangulo
x=p(1,:);y=p(2,:);z=p(3,:);
plot3(x,y,z,'b') % realiza la grafica del triangulo original
title('PROYECCION DE UN TRIANGULO SOBRE EL PLANO XY')
a=[1 0 0;0 1 0;0 0 0]; % introduce la matriz asociada a la transformacion lineal
pt=a*p; % Calcula la matriz pt cuyas columnas son las imagenes de los vertices del triangulo original
hold on % congela la ventana grafica
xt=pt(1,:);yt=pt(2,:);zt=pt(3,:); % xt,yt y zt son vectores fila que contienen las primeras, segundas y terceras componentes respectivamente de los vertices transformados
fill3(xt,yt,zt,'r') % dibuja el triangulo transformado y lo pinta de rojo
grid % añade cuadricula a la grafica
hold off % desactiva el hold
% El aula virtual de Algebra Lineal
si se lo ejecuta desde la ventana de comandos, produce el siguiente gráfico:
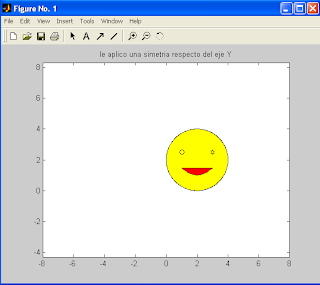
 Ejemplo 2: a una carita se le aplica una simetría respecto del eje Y
Ejemplo 2: a una carita se le aplica una simetría respecto del eje Y% la cara
t=-3:.01:3;x=2*cos(t)+2;y=2*sin(t)+2;
fill(x,y,'y')
axis([-8 8 0 8])
axis equal
hold on
% los ojos
plot(1,2.5,'ko');plot(3,2.5,'kh')
% la boca
x1=1:.1:3;y1=-cos(x1-2)+2;
fill(x1,y1,'r')
title('le aplico una simetria respecto del eje Y')
pause
a=[-1 0;0 1];
IC=a*[x;y]; % obtengo la imagen de la cara
IB=a*[x1;y1]; % obtengo la imagen de la boca
Iojos=a*[1 3;2.5 2.5]; % obtengo la imagen de los ojos
xim=IC(1,:);yim=IC(2,:);
x1im=IB(1,:);y1im=IB(2,:);
x1ojos=Iojos(1,1);y1ojos=Iojos(2,1);x2ojos=Iojos(1,2);y2ojos=Iojos(2:2);
fill(xim,yim,'y')
fill(x1im,y1im,'r')
plot(x1ojos,y1ojos,'ko');plot(x2ojos,y2ojos,'kh')
title('SIMETRIA RESPECTO DEL EJE Y')
hold off
% El aula virtual de Algebra Lineal
al ejecutarlo se obtienen los siguientes gráficos:
Ejemplo 3: archivo que dibuja una casa y le aplica diversas transformaciones lineales
H=[- 6 -6 -7 0 7 6 6 -3 -3 0 0 -6; -7 2 1 8 1 2 -7 -7 -2 -2 -7 -7];
x=H(1,:)';y=H(2,:)';plot(x,y);
axis([-10 10 -10 10]); axis('square');
pause
A=[cos(pi/4) -sin(pi/4);sin(pi/4) cos(pi/4)];
B=A*H;
x=B(1,:)';y=B(2,:)';plot(x,y); title('Rotacion de un angulo de 45º')
pause
A=[1 0;0 -1];
B=A*H;
x=B(1,:)';y=B(2,:)';plot(x,y); title('Simetría respecto OX')
pause
A=[-1 0;0 1];
B=A*H;
x=B(1,:)';y=B(2,:)';plot(x,y); title('Simetría respecto OY')
pause
A=[-1 0;0 -1];
B=A*H;
x=B(1,:)';y=B(2,:)';plot(x,y); title('Simetría respecto O')
pause
A=[0.5 0.2;0.2 0.5];
B=A*H;
x=B(1,:)';y=B(2,:)';plot(x,y);title('La deformamos')
al ejecutarlo, se observa la siguiente sucesión de gráficos:
También pueden aplicar transformaciones a curvas en el espacio, como por ejemplo:
Ejemplo 4: Expandimos una hélice
t = 0:pi/50:10*pi;
x=sin(t);y=cos(t);z=t;
plot3(x,y,z,'m');
title('HELICE')
hold on
grid
%Aplicamos la transformacion que la expande un factor K=2 en todas las direcciones
puntos=[x;y;z];
M=[2 0 0;0 2 0;0 0 2];
Im=M*puntos;
xim=Im(1,:);yim=Im(2,:);zim=Im(3,:);
plot3(xim,yim,zim,'r')
% El aula virtual de Algebra Lineal
al ejecutar este archivo, Matlab nos devuelve el siguiente gráfico:
%_________________________________________________________________
% Archivo de funcion que permite aplicar diversas transformaciones % lineales a
% una figura dada, ingresando la matriz asociada desde el teclado
%_________________________________________________________________
disp(' __________________________________________________________')
disp('| Archivo de funcion que permite aplicar diversas transformaciones |')
disp('| lineales a una figura dada, ingresando la matriz asociada |')
disp('| desde el teclado |')
disp(' |El aula virtual de Álgebra Lineal |')
disp(' __________________________________________________________')
A=input('Ingrese la matriz asociada a la transformacion lineal de R2 en R2: ')
% dibuja la cara
t=-3:.01:3;x=cos(t)+1;y=sin(t)+1;
plot(x,y,'r')
grid
axis equal
hold on
% dibuja el cuerpo
x1=[4 1 0 1 1 1 -1 1 3 4];y1=[-2 0 -2 -3 0 -4 -8 -4 -5 -8];
plot(x1,y1,'r')
% forma la matriz de puntos
Pcara=[x;y];Pcuerpo=[x1;y1];
% aplica una transformacion lineal de R2 en R2 cuya matriz asociada es la ingresada A
Imcara=A*Pcara;
Imcuerpo=A*Pcuerpo; xim=Imcara(1,:);yim=Imcara(2,:);x1im=Imcuerpo(1,:);y1im=Imcuerpo(2,:); plot(xim,yim,x1im,y1im,'b')
hold off
% El aula virtual de Algebra Lineal
la figura original es la siguiente:
Éstos son algunos ejemplos sencillos de lo que pueden realizar. En este blog pueden encontrar otros que han sido confeccionados por alumnos que ya cursaron la asignatura.
Para el trabajo integrador con Matlab se les solicita que:
- Investiguen sobre los operadores y expresiones booleanas y las estructuras de control if… else , for, while.
- Confeccionen un pequeño programa con Matlab (archivo .m de función) referido a la aplicación de transformaciones lineales a figuras en el plano o el espacio
Deberán presentar un informe por escrito que contenga:
- el tema específico de Álgebra Lineal que han abordado,
- una explicación del funcionamiento del programa,
- el código fuente del programa,
- un ejemplo concreto de su aplicación (es decir, una prueba de su funcionamiento)
Deberán acompañar el informe con un disquete que contenga el archivo.
Como material de consulta extra, cuentan con los enlaces indicados en este blog y el manual de Matlab que se encuentra disponible en la biblioteca del Departamento de Matemática.
Saludos
 la profe
la profe


















hola profe, luego de mirar las notas el viernes, y notar mi no aprobacion (50 ptos), me invadio la duda de como mirar el parcial no aprobado, asi ver mis fallas
¡¡¡Cómo no me di cuenta!!!!
Los parciales quedaron en mi oficina. Algunos alumnos los consultaron el viernes, tuve la intensión de traerlos a mi casa, pero me los olvidé. Lamentablemente la universidad está cerrada y no creo que pueda buscarlos.
De todos modos haré un listado de los errores que encontré con más frecuencia en los exámenes (igualmente puede ver el parcial cuando nos reintegremos).
ERRORES:
1- La mayoría de los alumnos tuvieron desaciertos en el Verdadero o Falso, lo que implica que deben reforzar los conceptos teóricos.
2- En muchos casos confundieron la ecuación vectorial de la recta con la del plano y cuando se les solicitó que determinen las intersecciones de un plano dado con los planos de coordenadas lo hicieron con los ejes (¿esto puede ser porque no leyeron bien el enunciado?)
3- Con respecto a las transformaciones lineales algunos no hicieron nada, ¿quizás porque les di la matriz asociada? También tienen problemas con los elementos del núcleo o de la imagen al no comprender a cuál de los espacios vectoriales pertenecen (¿al de partida o al de llegada?). Por supuesto que esto influye también cuando tienen que aplicar el teorema de las dimensiones y vincular las transformaciones lineales con los sistemas de ecuaciones.
4- En la diagonalización de matrices las fallas más frecuentes están vinculadas al calculo erróneo del det(lambda I – A) y por lo tanto los valores encontrados no son los valores propios de A. Luego resuelven mal los sistemas de ecuaciones lineales correspondientes y si lo hacen bien, no se dan cuenta que llegan a resultados incoherentes como por ejemplo que el espacio propio asociado a un valor propio es {0v}. Hubo casos en los que hallaron que la matriz que diagonaliza a la matriz dada es rectangular (¿cómo podría ser inversible una matriz no cuadrada?) o tiene una fila o columna de ceros (no siendo inversible).
En síntesis, les aconsejo que:
- Repasen los conceptos teóricos.
- Revean las herramientas básicas necesarias para resolver exitosamente los ejercicios: matrices, determinantes, sistemas de ecuaciones lineales.
- Lean detenidamente y varias veces el enunciado de un ejercicio o problema hasta estar seguros de haber comprendido lo que se les pide.
- Revisen si el resultado obtenido es factible y en el caso que sea posible verifíquenlo.
Saludos y estoy dispuesta a responder sus preguntas.
Hola profe, muy buena su pagina jiji
Tenemos un video interesante sobre matlab para algebra lineal si desean pueden chequearlo aqui
Buenas noches prof, mi nombre es elizabeth vargas de venezuela y dicto algebra lineal en la unexpo-puerto ordaz: mis alumnos practicamente comenten los mismos errores.
gracias
Elizabeth
Hola Elizabeth y un saludo para todos los venezolanos.
Cuando uno comparte con colegas de otras universidades sus experiencias, observa que las dificultades que presentan los estudiantes son las mismas, más allá de los contextos educativos diferentes. Esto debería ponernos en alerta para reconsiderar el cómo enseñamos y de esa manera disminuir las falencias que los lleva a cometer los mismos errores.
Gracias por tu comentario y por visitarnos.
disculpa una inquietud.. me enviaron un trabajo de hallar una aplicacion en matlab... que utilice transformaciones lineales .. hasta ahi bien! pero me dice que la demuestre!! como hago eso!! ayudame de urgencia
Hola estoy en 4to de secundaria y tengo una tarea sobre 10 situaciones en imagenes donde se aplique la homotecia central con 01.
sera que me puedes ayudar con el ejercicio de la elipse quiero agregarlo a un GUI y poner un edittext y al momento de ejecutarlo poner una ecuación cualquiera y que grafique la funcion